Introduction to Turbofan

about the sea of node

google document about turbofan and SoN

lecture about SoN(TODO)

v8的优化过程都是基于sea of node这种IR进行的，所以在学习v8的优化过程之前需要先对sea of node有一些了解。

通过cliff click 1993年的一篇论文和网上的一些资料可以对SoN有一定的了解，当然对于SoN在优化时的具体操作方法，以及在优化结束之后如何由sea of node重新构建CFG这些还不太清楚。

V8将byte code转换为图形式的sea of node并在sea of node上进行优化。sea of node是一种图形式的IR它有下面的特点：

• sea of node没有BB这种结构，指令作为图中的node，整个方法中的node构成一张大图。这样基于sea of node的优化都是全局的。
• sea of node是SSA形式的，且数据依赖被直接保存在指令中，和llvm IR很相似，可以直接访问use-def链且use-def链非常简单。
• 在sea of node中除了被控制流链接起来的控制结点（start，region，IF）这些结点的是固定的，其他的指令因为缺少了基本块的束缚都是浮动的，可以在全局内进行移动。但是这些结点的移动也不是任意进行的，这些副作用结点之间有自己的依赖关系（先读后写，如果被调度为先写后读，那么读出的内容就会发生变化），只有在依赖满足时才可以执行副作用指令。

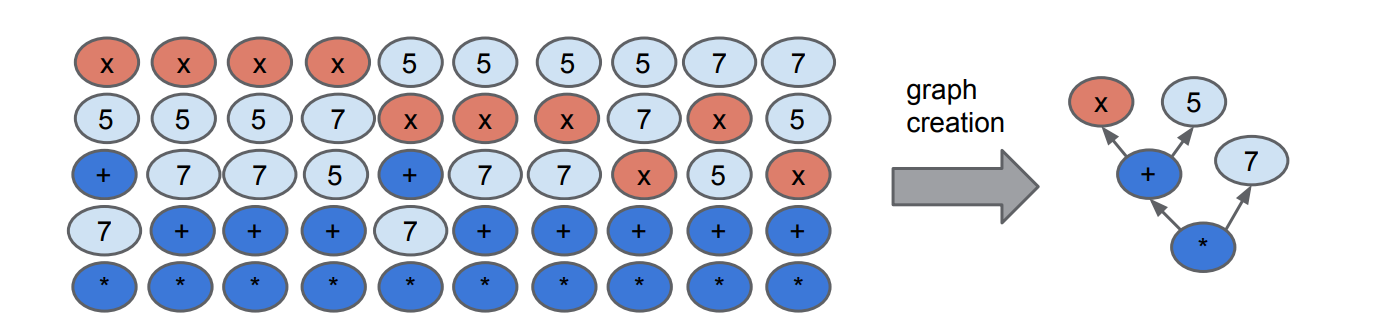
上面的图中是线性IR和SoN之间的转换关系，一个sea of node转化为线性IR可以很多种情况，这也表明sea of node中的结点有很高的可调度性。

实际上正是因为sea of node中结点组织关系的松散（在llvm IR中进行transformation时要不断的在BB中删除插入指令）在基于sea of node进行大部分优化时只需要进行边的连接和删除，这样可以大量的节省优化所需的时间。且因为sea of node松散的组织结构，优化器可以通过schedule这些node的位置来获得最好的优化效果（减小寄存器调度的压力，配合CPU流水线），并且在sea of node中schedule的过程相对于线性IR要简单很多。

之后来看看在不同阶段turbofan对于sea of node的优化过程。

turbofan optimization

V8 version: 7.0.276.3

使用下面这个JS代码片段作为例子，通过观察turbofan对于这段代码片段的优化过程学习turbofan的优化流程。

function opt_me() {
  let x = Math.random();
  let y = x + 2;
  return y + 3;
}

在turbofan的优化过程中首先会将字节码转换为sea of node，v8开发团队提供了名为turbolizer的工具可以查看sea of node在turbofan优化各个阶段的状态。使用turbolizer有两个步骤：

• 首先构建turbolizer，turbolizer使用下面的命令构建：

#tools/turbolizer/ 
cd tools/turbolizer
npm i
npm run-script build
python -m SimpleHTTPServer

然后用浏览器访问对应的端口就可以进入turbolizer的界面。

• 另外在使用turbolizer的时候需要由v8生成的.cfg和.json文件。需要在d8执行JS代码时加上–trace-turbo这个参数，在代码执行结束后就会生成这两个文件。将这两个文件加载到turbolizer中就可以观察在不同优化通道中sea of node的图形视图。

按不同优化通道的优化顺序来观察turbofan对上面opt_me()函数的优化，首先是Graph build阶段，这个阶段负责生成未优化的sea of node，下面是从turbolizer中截取的有关函数逻辑的生成图：

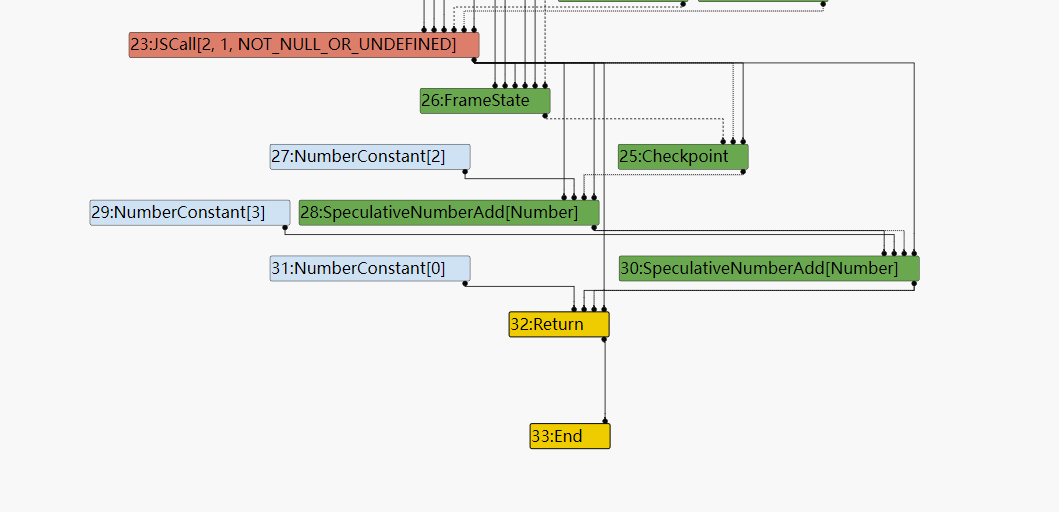
• 一次JSCall代表了对Math.random()这个函数的调用。
• 两次SpeculativeNumberAdd代表了两次加法运算。

下面就要正式进入turbofan的优化阶段。

Typer phase

source code analysis

在SoN构造完成之后会对SoN进行Typer phase。Typer phase也是turbofan推测优化的一部分它负责为每个结点赋予可能的Type, Typer直接从node类型综合操作数等其他信息，推断出预期的Type。有了Type就可以针对特定的Type对SoN进一步优化。

Typer phase由createGraph()调用，在SoN构造完成之后负责为图中的每个结点关联上预测的类型。

//pipeline.cc
// Type the graph and keep the Typer running on newly created nodes within
// this scope; the Typer is automatically unlinked from the Graph once we
// leave this scope below.
Typer typer(isolate(), data->js_heap_broker(), flags, data->graph());
Run<TyperPhase>(&typer);
RunPrintAndVerify(TyperPhase::phase_name());

Run<TyperPhase>(&typer)会调用TyperPhase类的Run()函数，然后再由TyperPhase的Run()函数最终调用Typer的Run()函数。在Typer的Run()函数中使用Typer对象初始化一个Visitor，并用这个访问者去遍历所有的Node。visitor的Reduce（）函数负责对每个Node进行Typer reduce。

//typer.cc
void Typer::Run(const NodeVector& roots,
                LoopVariableOptimizer* induction_vars) {
  if (induction_vars != nullptr) {
    induction_vars->ChangeToInductionVariablePhis();
  }
  Visitor visitor(this, induction_vars);//创建一个visitor
  GraphReducer graph_reducer(zone(), graph());
  graph_reducer.AddReducer(&visitor);//在Reducer vector中添加Typer Reducer
  for (Node* const root : roots) graph_reducer.ReduceNode(root);//遍历start？
  graph_reducer.ReduceGraph();//使用Reducer vector中的Reducer遍历图中的所有结点进行Reduce操作

  if (induction_vars != nullptr) {
    induction_vars->ChangeToPhisAndInsertGuards();
  }
}

在Typer的Visitor的Reducer()函数中使用一个大的Switch case结构来根据node的opcode将当前正在遍历的node分发到对应的Typer函数去处理：

//typer.cc
Reduction Reduce(Node* node) override {
    if (node->op()->ValueOutputCount() == 0) return NoChange();
    //dispatch the node!
    switch (node->opcode()) {
#define DECLARE_CASE(x) \
  case IrOpcode::k##x:  \
    return UpdateType(node, TypeBinaryOp(node, x##Typer));
      JS_SIMPLE_BINOP_LIST(DECLARE_CASE)
#undef DECLARE_CASE

#define DECLARE_CASE(x) \
  case IrOpcode::k##x:  \
    return UpdateType(node, Type##x(node));
      DECLARE_CASE(Start)
      DECLARE_CASE(IfException)
      // VALUE_OP_LIST without JS_SIMPLE_BINOP_LIST:
      COMMON_OP_LIST(DECLARE_CASE)
      SIMPLIFIED_COMPARE_BINOP_LIST(DECLARE_CASE)
	  ……
#undef DECLARE_CASE

#define DECLARE_CASE(x) \
  case IrOpcode::k##x:  \
    return UpdateType(node, TypeBinaryOp(node, x));
      SIMPLIFIED_NUMBER_BINOP_LIST(DECLARE_CASE)
      SIMPLIFIED_SPECULATIVE_NUMBER_BINOP_LIST(DECLARE_CASE)
#undef DECLARE_CASE
……

根据node的opcode的类型将调用对应的Typer函数：如果node的opcode类型为JSCall（根据上面的例子）那么调用的Typer函数就是JSCallTyper()。之后进入JSCallTyper()这个函数中看一下：

Type Typer::Visitor::JSCallTyper(Type fun, Typer* t) {
  if (!fun.IsHeapConstant() || !fun.AsHeapConstant()->Ref().IsJSFunction()) {
    return Type::NonInternal();
  }
  JSFunctionRef function = fun.AsHeapConstant()->Ref().AsJSFunction();
  if (!function.shared().HasBuiltinFunctionId()) {
    return Type::NonInternal();
  }
  switch (function.shared().builtin_function_id()) {
    case BuiltinFunctionId::kMathRandom:
      return Type::PlainNumber();
    case BuiltinFunctionId::kMathFloor:
    ……

从上面的源码中可以看到，JSCallTyper()这个函数首先判断由JSCall调用的函数是否为内置函数，如果是内置函数的，就可以将JSCall与所调用内置函数的预期返回值类型关联起来。在上面的opt_me()函数中调用了 Math.random()这个builtin函数，Typer预期这个内置函数返回值类型是PlainNumber，所以在Typer结束后这个JSCall node将被打上PlainNumber的标签。

之后Typer会对NumberConstant这个结点进行处理。处理过程在TypeNumberConstant()这个函数中：

Type Typer::Visitor::TypeNumberConstant(Node* node) {
  double number = OpParameter<double>(node->op());
  return Type::NewConstant(number, zone());
}


Type Type::NewConstant(double value, Zone* zone) {
  if (RangeType::IsInteger(value)) {
    return Range(value, value, zone);
  } else if (IsMinusZero(value)) {
    return Type::MinusZero();
  } else if (std::isnan(value)) {
    return Type::NaN();
  }

  DCHECK(OtherNumberConstantType::IsOtherNumberConstant(value));
  return OtherNumberConstant(value, zone);
}

在TypeNumberConstant()中首先取出node所代表的常量值value，之后传入NewConstant这个函数中。在NewConstant中负责根据value的值来返回对应的Type：

• 如果value的值为整形，那么返回一个range类型，range类型的是带有范围的整形。
• 如果value的值为-0，返回MinusZero类型。
• 如果是NaN，还返回NaN类型。
• 以上都不成立的话那value应该是一个浮点型的值，所以返回OtherNumberConstant Type。

然后Typer将处理SpeculativeNumberAdd类型的结点。在Typer的visitor的Reduce()中被调用的是，TypeBinaryOp()这个函数：

#define DECLARE_CASE(x) \
  case IrOpcode::k##x:  \
    return UpdateType(node, TypeUnaryOp(node, x));
      SIMPLIFIED_NUMBER_UNOP_LIST(DECLARE_CASE)
      SIMPLIFIED_SPECULATIVE_NUMBER_UNOP_LIST(DECLARE_CASE)
#undef DECLARE_CASE

在TypeBinaryOp()中会将二元指令的两个操作数的Type都取出来，然后调用SpeculativeNumberAdd()。

Type Typer::Visitor::TypeBinaryOp(Node* node, BinaryTyperFun f) {
  Type left = Operand(node, 0);//取第一个操作数的Type
  Type right = Operand(node, 1);//取第二个操作数的Type
  return left.IsNone() || right.IsNone() ? Type::None()
                                         : f(left, right, typer_);
}

在SpeculativeNumberAdd()先尝试将两个操作数的Type转换为Number,Number包括所有smi、double、uint32、-0.0、NaN。因为SpeculativeNumberAdd左右两个操作数一个是Range属于Number(NumberConstant结点)，另一个是PlainNumber(JSCall结点)也属于Number所以直接返回原Type。，保存在lhs和rhs里。

#define SPECULATIVE_NUMBER_BINOP(Name)                         \
  Type OperationTyper::Speculative##Name(Type lhs, Type rhs) { \
    lhs = SpeculativeToNumber(lhs);                            \
    rhs = SpeculativeToNumber(rhs);                            \
    return Name(lhs, rhs);                                     \
  }
SPECULATIVE_NUMBER_BINOP(NumberAdd)

最后用lhs和rhs中返回的Type调用NumberAdd()计算结点SpeculativeNumberAdd的Type，在NumberAdd()中检查一些极端情况比如说操作数Type是不是MinusZero，NaN……根据之前的操作数Type，在左右操作数都属于PlanNumber的情况下，最终返回的Type还是PlainNumber。

Type type = Type::None();
  lhs = Type::Intersect(lhs, Type::PlainNumber(), zone());
  rhs = Type::Intersect(rhs, Type::PlainNumber(), zone());
  if (!lhs.IsNone() && !rhs.IsNone()) {
    if (lhs.Is(cache_.kInteger) && rhs.Is(cache_.kInteger)) {
      type = AddRanger(lhs.Min(), lhs.Max(), rhs.Min(), rhs.Max());
    } else {
      if ((lhs.Maybe(minus_infinity_) && rhs.Maybe(infinity_)) ||
          (rhs.Maybe(minus_infinity_) && lhs.Maybe(infinity_))) {
        maybe_nan = true;
      }
      type = Type::PlainNumber();
    }
  }

  // Take into account the -0 and NaN information computed earlier.
  if (maybe_minuszero) type = Type::Union(type, Type::MinusZero(), zone());
  if (maybe_nan) type = Type::Union(type, Type::NaN(), zone());
  return type;

在数字有关的Type关系如下，上面的Type推导都是根据下面Type之间的关系进行的：

V(PlainNumber,                  kIntegral32 | kOtherNumber) \
V(OrderedNumber,                kPlainNumber | kMinusZero) \
V(MinusZeroOrNaN,               kMinusZero | kNaN) \
V(Number,                       kOrderedNumber | kNaN) \

到现在为止整个Typer过程已经完成。

如下是经历了typer之后sea of node的图形化表示：

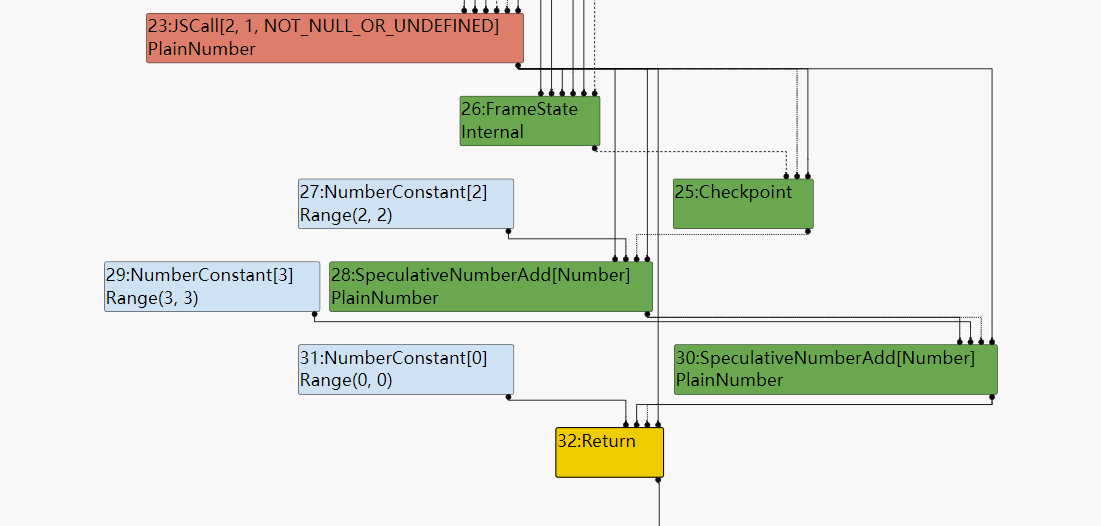
Typed lowering

经过Typer phase之后很多结点已经被打上Type，相当于一个动态类型语言（类型无法确定）到现在已经拥有了推测的类型，虽然类型可能并不精确，但是仍然是一个很大的进步。这些类型信息可以用于简化结点对应的操作，拿Add操作举例子：如果没有类型信息，add可以是number，string，object的加法，但是一旦有了推测的add类型，那么最终生成的机器码将专注于这一种类型这将删掉很多冗余操作。

所以在Typer phase之后关注的优化是Typed lowering，这个phase将根据结点的Type信息对node进一步简化。还是在createGraph()这个函数中在Run<TyperPhase>(&typer);之后将调用Typed Lowering:

//pipeline.cc CreateGraph()
// Lower JSOperators where we can determine types. 
Run<TypedLoweringPhase>();
RunPrintAndVerify(TypedLoweringPhase::phase_name());

和Typer phase一样外层的Run()最终会调用TypedLoweringPhase的Run()。

//pipeline.cc
void Run(PipelineData* data, Zone* temp_zone) {
    ……
    AddReducer(data, &graph_reducer, &dead_code_elimination);
    AddReducer(data, &graph_reducer, &duplicate_addition_reducer);
    AddReducer(data, &graph_reducer, &create_lowering);
    AddReducer(data, &graph_reducer, &constant_folding_reducer);
    AddReducer(data, &graph_reducer, &typed_optimization);
    AddReducer(data, &graph_reducer, &typed_lowering);
    AddReducer(data, &graph_reducer, &simple_reducer);
    AddReducer(data, &graph_reducer, &checkpoint_elimination);
    AddReducer(data, &graph_reducer, &common_reducer);
    graph_reducer.ReduceGraph();
  }

在TypedLoweringPhase的Run()中向Reducer Vector中添加了很多reducer。其中我比较关注的是Typed Opimization和Typed Lowering这两个redcuer。

• Typed Optimization：对SoN中的一些非JSNode进行优化，这个可能包括对一些CheckNode（CheckNode、CheckString……）的消除还有对一些Node（phi）的Type的化简。ReduceGraph()将调用TypedOptimization的Reduce()函数遍历整张图，在Redcue()函数中有一个很大的swicth case根据node的opcode来分发node到对应的优化函数。

  //typed-optimization.cc   TypedOptimization::Reduce()     
  	case IrOpcode::kCheckNumber:
        return ReduceCheckNumber(node);
      case IrOpcode::kCheckString:
        return ReduceCheckString(node);
      case IrOpcode::kCheckEqualsInternalizedString:
        return ReduceCheckEqualsInternalizedString(node);
      ……
      case IrOpcode::kNumberFloor:
        return ReduceNumberFloor(node);
      case IrOpcode::kNumberToUint8Clamped:
        return ReduceNumberToUint8Clamped(node);
      case IrOpcode::kPhi:
        return ReducePhi(node);
  

• 对于Typed Lowering来说ReduceGraph()将调用JSTypedLowering这个类的Reduce()函数。而在v8的注释中也很清楚的解释了JSTYpedLowering这个类的作用：

  // Lowers JS-level operators to simplified operators based on types.
  

  这个类主要是对JS-level的node进行化简。在它的Reduce函数中也有一个很大的switch case结构，负责根据node的opcode将node分发到对应的优化函数中。

  Reduction JSTypedLowering::Reduce(Node* node) {
    DisallowHeapAccess no_heap_access;
    
    switch (node->opcode()) {
      case IrOpcode::kJSEqual:
        return ReduceJSEqual(node);
      case IrOpcode::kJSStrictEqual:
        return ReduceJSStrictEqual(node);
      case IrOpcode::kJSLessThan:         // fall through
      case IrOpcode::kJSGreaterThan:      // fall through
      case IrOpcode::kJSLessThanOrEqual:  // fall through
      case IrOpcode::kJSGreaterThanOrEqual:
        return ReduceJSComparison(node);
  

SpeculativeNumberAdd Typed Lowering

之后具体的来看一下在Typed Lowering这个阶段是如何对SpeculativeNumberAdd()这个node进行优化的。这个node属于JS-level的node，所以它应该在JSTypedLowering的Reduce()中被优化.

case IrOpcode::kSpeculativeNumberAdd:
      return ReduceSpeculativeNumberAdd(node);

Reduce()调用ReduceSpeculativeNumberAdd()。

Reduction JSTypedLowering::ReduceSpeculativeNumberAdd(Node* node) {
  JSBinopReduction r(this, node);
  NumberOperationHint hint = NumberOperationHintOf(node->op());
  if ((hint == NumberOperationHint::kNumber ||
       hint == NumberOperationHint::kNumberOrOddball) &&
      r.BothInputsAre(Type::PlainPrimitive()) &&
      r.NeitherInputCanBe(Type::StringOrReceiver())) {
    // SpeculativeNumberAdd(x:-string, y:-string) =>
    //     NumberAdd(ToNumber(x), ToNumber(y))
    r.ConvertInputsToNumber();
    return r.ChangeToPureOperator(simplified()->NumberAdd(), Type::Number());
  }
  return NoChange();
}

• 首先从判断node的hint是什么：因为在SoN中的两个SpeculativeNumberAdd都是PlainNumber类型，所以得到的hint是Number。

• 然后判断两个操作数是否是PlainPrimitive类型：PlainPrimitive包括Number,String,Boolean，而所有的SpeculativeNumberAdd的操作数都属于Number，所以这个判断为真。

  V(PlainPrimitive,               kNumber | kString | kBoolean | \
                                    kNullOrUndefined) \
  

在前面的条件都满足的情况下，调用convertInputsToNumber()先将操作数都转换为Number类型，这个函数将其他类型的PlainPrimitive类型的Node转换为Number类型的Node，其中可能向SoN中替换Node或者插入ToNumber的Node。

最后用一个NumberAdd的Node替换SpeculativeNumberAdd。

经过Typed Lowering和Constant Folding之后的SoN：

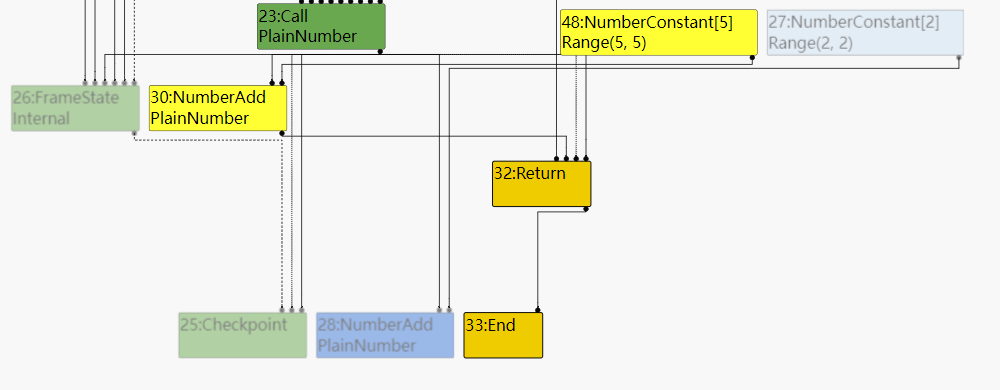
SpeculativeNumberAdd已经被转化为NumberAdd且+2+3已经被折叠为+5。

JSCall Typed Lowering

然后是对JSCall的Typed Lowering。

//js-typed-lowering.cc
Reduction JSTypedLowering::ReduceJSCall(Node* node) {
  DCHECK_EQ(IrOpcode::kJSCall, node->opcode());
  CallParameters const& p = CallParametersOf(node->op());
  int const arity = static_cast<int>(p.arity() - 2);
  ConvertReceiverMode convert_mode = p.convert_mode();
  Node* target = NodeProperties::GetValueInput(node, 0);
  Type target_type = NodeProperties::GetType(target);
  Node* receiver = NodeProperties::GetValueInput(node, 1);
  Type receiver_type = NodeProperties::GetType(receiver);
  Node* effect = NodeProperties::GetEffectInput(node);
  Node* control = NodeProperties::GetControlInput(node);

先从node中取出data dependency，control information， effect dependency。从这个取出的过程可以了解到JSCall这个opcode的第一个操作数是调用的目标函数，第二个操作数是调用过程的receive object。

//js-typed-lowering.cc
	[……]	
// Check if {target} is a known JSFunction.
  if (target_type.IsHeapConstant() &&
      target_type.AsHeapConstant()->Ref().IsJSFunction()) {
    JSFunctionRef function = target_type.AsHeapConstant()->Ref().AsJSFunction();
    SharedFunctionInfoRef shared = function.shared();

    [……]
    // Load the context from the {target}.
    Node* context = effect = graph()->NewNode(
        simplified()->LoadField(AccessBuilder::ForJSFunctionContext()), target,
        effect, control);
    NodeProperties::ReplaceContextInput(node, context);

    [……]

    // Update the effect dependency for the {node}.
    NodeProperties::ReplaceEffectInput(node, effect);

    // Compute flags for the call.
    CallDescriptor::Flags flags = CallDescriptor::kNeedsFrameState;
    Node* new_target = jsgraph()->UndefinedConstant();
    Node* argument_count = jsgraph()->Constant(arity);

    if (NeedsArgumentAdaptorFrame(shared, arity)) {
     [……]
    } else if (shared.HasBuiltinId() &&
               Builtins::HasCppImplementation(shared.builtin_id())) {
      // Patch {node} to a direct CEntry call.
      ReduceBuiltin(jsgraph(), node, shared.builtin_id(), arity, flags);
    } else if (shared.HasBuiltinId() &&
               Builtins::KindOf(shared.builtin_id()) == Builtins::TFJ) {
      // Patch {node} to a direct code object call.
      Callable callable = Builtins::CallableFor(
          isolate(), static_cast<Builtins::Name>(shared.builtin_id()));
      CallDescriptor::Flags flags = CallDescriptor::kNeedsFrameState;

      const CallInterfaceDescriptor& descriptor = callable.descriptor();
      auto call_descriptor = Linkage::GetStubCallDescriptor(
          graph()->zone(), descriptor, 1 + arity, flags);
      Node* stub_code = jsgraph()->HeapConstant(callable.code());
      node->InsertInput(graph()->zone(), 0, stub_code);  // Code object.
      node->InsertInput(graph()->zone(), 2, new_target);
      node->InsertInput(graph()->zone(), 3, argument_count);
      NodeProperties::ChangeOp(node, common()->Call(call_descriptor));
    } 

这里有一点不太懂就是注释里说的“is a known JSFunction”是什么意思，是指非用户定义函数么？

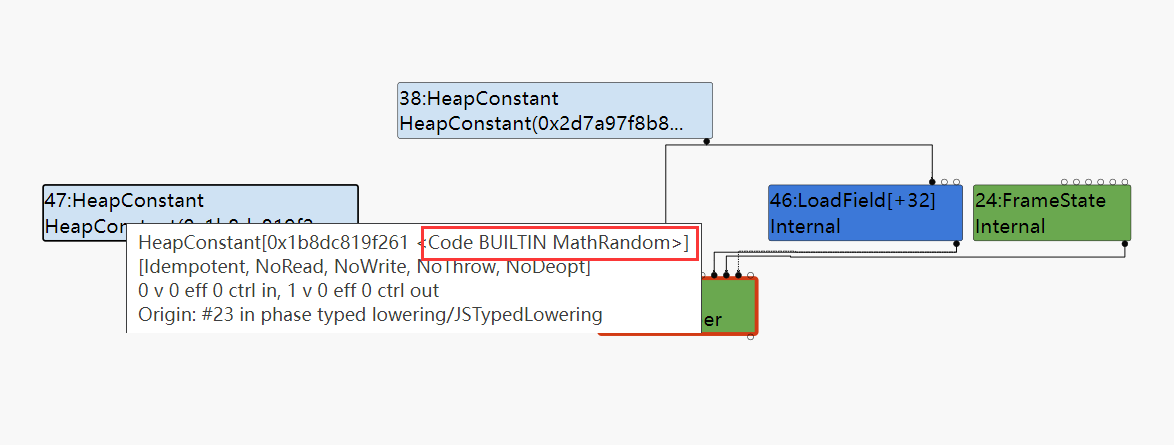
在例子中这个JSCall所调用的是Math.random()这个函数是一个由Code Stub Assembler所编写的内置函数。首先会为JSCall创建一个LoadField结点用于从JSFunction中获取函数调用的上下文。

然后判断当前调用的函数是否是由CSA内置函数，如果是的话就取出对应BuiltinID的内置函数，再从内置函数中取出可执行代码的地址stub_code,将stub_code作为JSCall的第一个参数（target）插入到node的input中。最后将node的opcode修改为Call。这样一个Math.random()的JSCall就优化完了。从JSCall到Call，这个过程降低了操作的复杂度。

下面是经过Typed Lowering之后这一次函数调用的图形化表示，可以看到第一个操作数已经被修改为Builtin function的code。

Range Type

在之前的分析中我们已经看到了许多次Range这个Type，但是看到的都是Range(n, n)这样的形式的Range。但是实际上Range可以有很多种形状，且在Turbofan中经常对代表算数运算的Node的Range Type进行合并，拿下面这段JS代码举个例子：

function opt_me(b) {
  let x = 10; // [1] x0 = 10
  if (b == "foo")
    x = 5; // [2] x1 = 5
  // [3] x2 = phi(x0, x1)
  let y = x + 2;
  y = y + 1000; 
  y = y * 2;
  return y;
}

opt_me("foo");

%OptimizeFunctionOnNextCall(opt_me);

opt_me("foo");

先看以下在未进行优化之前的SoN长什么样子：

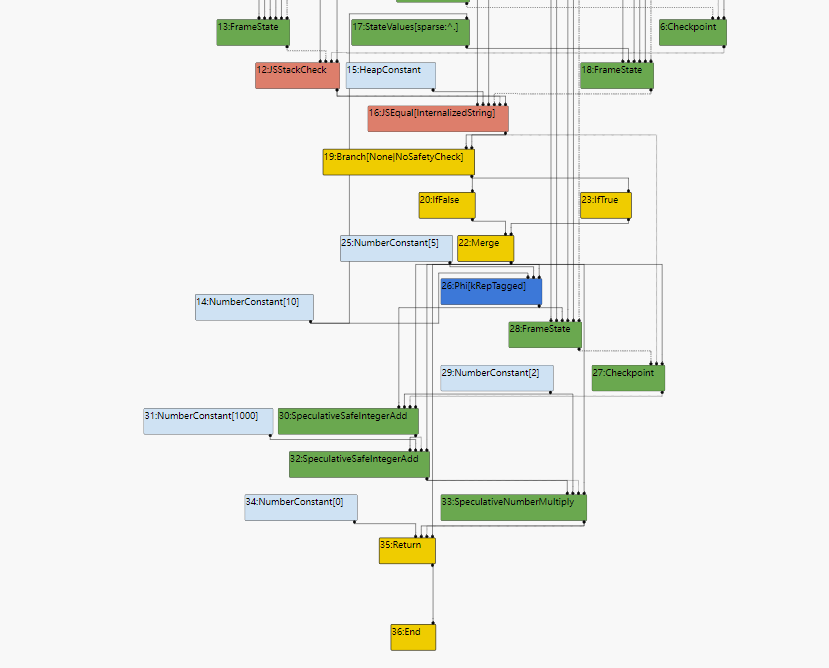
源码中的加法对应到SoN中是SpeculativeSafeIntegerAdd这样的Node，之所以产生这样的Node而不产生和之前一样SpeculativeNumberAdd的Node的原因是因为Speculative Optimization。

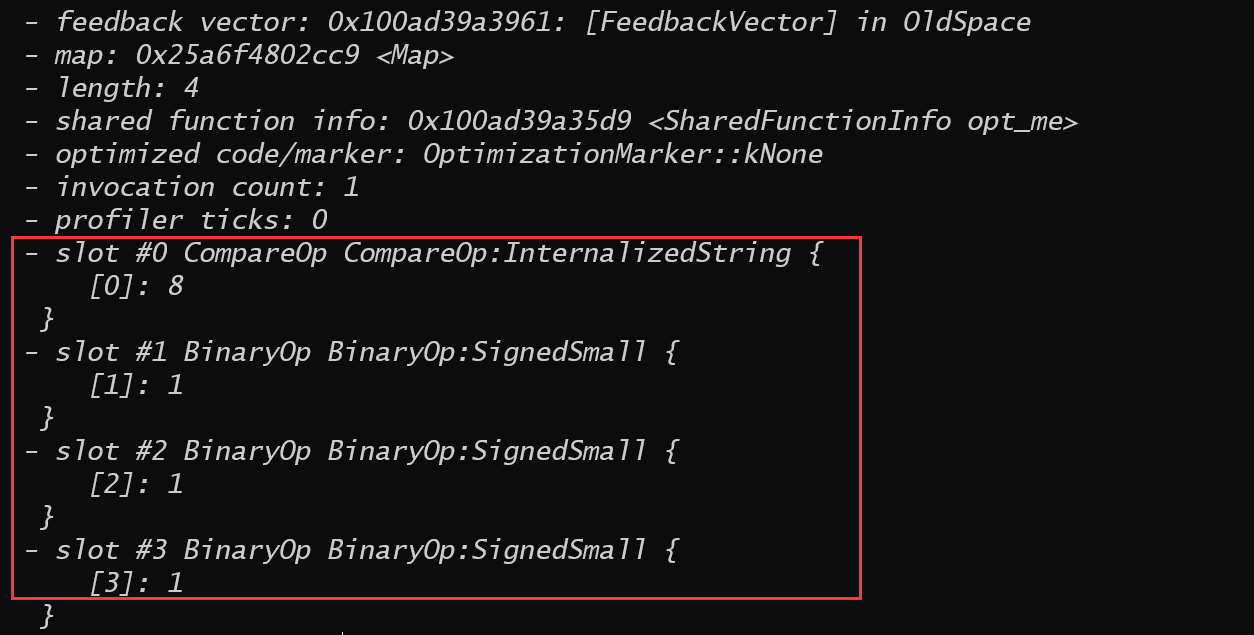
• 在优化前进行的那一次调用中传入的是一个smi，这样Ignition在收集feedback时，加法的Type feedback就被设置为smi。
• 之后opt_me被送入turbofan进行优化构建SoN时，turbofan就会参考feed back中的Type information生成SoN中的结点而smi对应的就是SpeculativeSafeIntegerAdd。

从打印出的feedback vector也可以看出这种情况：

phi Node Typer

继续回到range，我们先来看一下SoN中的phi Node，这个phi Node用于merge两个x的值，当传入的字符串为”foo“时x3 = x2 = 5，否则x3 = x1 = 10。在SoN中x1和x2都表示为NumberConstant，所以x1的Type是Range(10,10),x2的Type是Range(5,5)。关注于phi的Type我们通过阅读代码来推导一下。

Typer的Reduce()将会调用TypePhi()这个函数对phi Node进行Typer。

Type Typer::Visitor::TypePhi(Node* node) {
  int arity = node->op()->ValueInputCount();
  Type type = Operand(node, 0);
  for (int i = 1; i < arity; ++i) {
    type = Type::Union(type, Operand(node, i), zone());
  }
  return type;
}

这个函数的逻辑就是将phi Node的所有输入的Type都Union起来得到的Type就是phi Node的Type。将Range(5,5)和Range(10,10)Union起来之后就是Range(5,10)。这样就完成了对于phi Node对于Range的计算，最终的Type就是Range(5,10)。

之后这个Type将继续沿着计算的路线向下传递，然后就是SpeculativeSafeIntegerAdd中对于Range的计算。

SpeculativeSafeIntegerAdd Typer

SpeculativeSafeIntegerAdd的Typer过程和上面的SpeculativeAdd的Typer过程很一样（因为都是推测结点）。先从左右操作数中获得Type，对于let y = x + 2;这条语句来说生成的Node的左右操作数的Type都是Range（Rang(5, 10),Range(2, 2)），然后进入经过SpeculativeToNumber()返回的还是原Type。最后进入NumberAdd()。

上面分析对SpeculativeNumberAdd()进行Typer的时候分析过这个函数，处理一些极端情况-0.0和NaN之后，当两个操作数的Type都是Range的时候会进入下面的分支：

  Type type = Type::None();
  lhs = Type::Intersect(lhs, Type::PlainNumber(), zone());
  rhs = Type::Intersect(rhs, Type::PlainNumber(), zone());
  if (!lhs.IsNone() && !rhs.IsNone()) {
    if (lhs.Is(cache_.kInteger) && rhs.Is(cache_.kInteger)) {
      type = AddRanger(lhs.Min(), lhs.Max(), rhs.Min(), rhs.Max());//get into this branch
    } else {
      if ((lhs.Maybe(minus_infinity_) && rhs.Maybe(infinity_)) ||
          (rhs.Maybe(minus_infinity_) && lhs.Maybe(infinity_))) {
        maybe_nan = true;
      }
      type = Type::PlainNumber();
    }
  }

AddRange()函数是计算两个携带Range的Node相加之后的Node的Range：

Type OperationTyper::AddRanger(double lhs_min, double lhs_max, double rhs_min,
                               double rhs_max) {
  double results[4];
  results[0] = lhs_min + rhs_min;
  results[1] = lhs_min + rhs_max;
  results[2] = lhs_max + rhs_min;
  results[3] = lhs_max + rhs_max;
  // Since none of the inputs can be -0, the result cannot be -0 either.
  // However, it can be nan (the sum of two infinities of opposite sign).
  // On the other hand, if none of the "results" above is nan, then the
  // actual result cannot be nan either.
  int nans = 0;
  for (int i = 0; i < 4; ++i) {
    if (std::isnan(results[i])) ++nans;
  }
  if (nans == 4) return Type::NaN();
  Type type = Type::Range(array_min(results, 4), array_max(results, 4), zone());
  if (nans > 0) type = Type::Union(type, Type::NaN(), zone());
  // Examples:
  //   [-inf, -inf] + [+inf, +inf] = NaN
  //   [-inf, -inf] + [n, +inf] = [-inf, -inf] \/ NaN
  //   [-inf, +inf] + [n, +inf] = [-inf, +inf] \/ NaN
  //   [-inf, m] + [n, +inf] = [-inf, +inf] \/ NaN
  return type;
}

计算的逻辑是用两个Range的四个边界（lhs_min,lhs_max,rhs_min,rhs_max）互相相加得到四个结果，取四个结果中最小的作为相加之后Range的下界，四个结果中最大的作为相加之后的上界。其中还包含一些对infinite和NaN的处理。

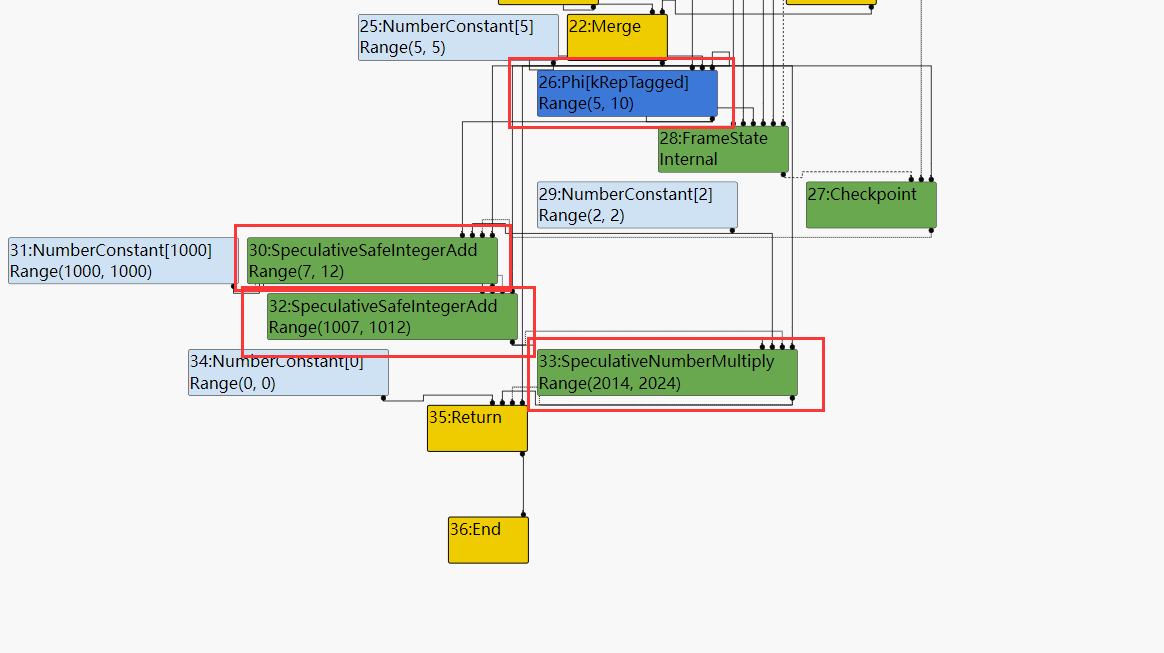
所以对于let y = x + 2;这条语句生成的SpeculativeSafeIntegerAdd Node在AddRange()经过计算得到的上界是10 + 2 = 12；而下界是 5 + 2 = 7；所以最终得到这个Node的Type是Range(7, 12)。依次类推之后的每个SpeculativeSafeIntegerAdd Node的Type都是这样计算的。

从最终得到的SoN中也可以看到结果是正确的：

CheckBounds

之后来认识一下SoN中另一类结点CheckBounds，CheckBounds的作用是在进行load和store之前对这两个动作的索引进行检查，以防止对内存的越界读写。

下面是一个会生成CheckBounds Node的例子，左边是JS源码而右边是生成的SoN的结点

function opt_me(b) {
  let values = [42,1337];       // HeapConstant <FixedArray[2]>
  let x = 10;                   // NumberConstant[10]          | Range(10,10)
  if (b == "foo")
    x = 5;                      // NumberConstant[5]           | Range(5,5)
                                // Phi                         | Range(5,10)
  let y = x + 2;                // SpeculativeSafeIntegerAdd   | Range(7,12)
  y = y + 1000;                 // SpeculativeSafeIntegerAdd   | Range(1007,1012)
  y = y * 2;                    // SpeculativeNumberMultiply   | Range(2014,2024)
  y = y & 10;                   // SpeculativeNumberBitwiseAnd | Range(0,10)
  y = y / 3;                    // SpeculativeNumberDivide     | PlainNumber[r][s][t]
  y = y & 1;                    // SpeculativeNumberBitwiseAnd | Range(0,1)
  return values[y];             // CheckBounds                 | Range(0,1)
}

最后的Array getter在进入turbofan进行优化时将会生成一个CheckBounds Node，用于检查访问数组索引是否越界。在turbolizer打印出的SoN中也可以看到这一点：

• CheckBounds的第一个输入是访问数组使用的索引，也就是即将被check的值。
• CheckBounds的第二个输入是数组的长度，也就是check时使用的上界。

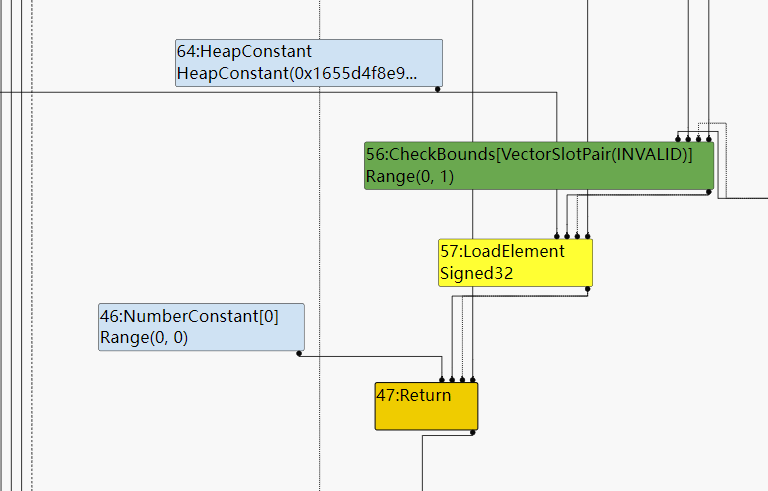
在图中可以看到CheckBound Node的Type是Range(0,1)，而这个Type是在TypeCheckBound()函数中生成，我们来具体研究一下这个函数的源码：

Type Typer::Visitor::TypeCheckBounds(Node* node) {
  Type index = Operand(node, 0);
  Type length = Operand(node, 1);
  DCHECK(length.Is(Type::Unsigned31()));
  if (index.Maybe(Type::MinusZero())) {
    index = Type::Union(index, typer_->cache_.kSingletonZero, zone());
  }
  index = Type::Intersect(index, Type::Integral32(), zone());
  if (index.IsNone() || length.IsNone()) return Type::None();
  double min = std::max(index.Min(), 0.0);
  double max = std::min(index.Max(), length.Max() - 1);
  if (max < min) return Type::None();
  return Type::Range(min, max, zone());
}

• 首先从函数可以给我们的提示是CheckBounds的第一个操作数是要被检查的index Node，而第二个操作数是即将被访问的数组的length Node，首先取出这两个结点的Type。
  • 在上面的例子中index为y而y在访问之前和1做与运算，所以它的Type是Range(0,1)。
  • 而数组的length本来是从数组的object中load出来，但是经过load elimination之后变成一个常数constant 2。
• 然后处理了一些极端的情况：negative zero，NaN……
• 然后开始计算CheckBounds的Type，我在没有仔细看源码之前以为CheckBounds的Range就是（0, length）。但实际上不是这样：
  • CheckBounds的Range的最小值是0和Index Range最小值中更大的那一个。
  • 而CheckBounds的Range的最大值是length和Index Range最大值中更小的那一个。

这个时候从利用的思路来考虑如果能在Turbofan优化之后将对于数组访问的这些CheckBounds优化掉，那么没有了CheckBounds的限制我们就可以随意对数组进行访问，甚至对数组进行越界读写。而turbofan还真的提供了这样的优化。

Simplified Lowering

在simpilfied lowering中将对冗余的CheckBounds进行消除，这个优化过程将在OptimizeGraph()函数中被调用。

  //pipeline.cc OptimizeGraph()
  // Perform simplified lowering. This has to run w/o the Typer decorator,
  // because we cannot compute meaningful types anyways, and the computed types
  // might even conflict with the representation/truncation logic.
  Run<SimplifiedLoweringPhase>();
  RunPrintAndVerify(SimplifiedLoweringPhase::phase_name(), true);

  // From now on it is invalid to look at types on the nodes, because the types
  // on the nodes might not make sense after representation selection due to the
  // way we handle truncations; if we'd want to look at types afterwards we'd
  // essentially need to re-type (large portions of) the graph.

OptimizeGraph()中的Run()将调用SimpifiledLoweringPhase这个类中的Run()函数之后 的调用链：Run() -->LoweringALLNodes-->RepresentationSelector::Run()--> VisitNod()。在VisitNode中使用一个大的switch case结构根据Node的Opcode将Node分发到对应的优化函数中。

下面是对于CheckBounds类型的Node的处理过程。

 case IrOpcode::kCheckBounds: {
        const CheckParameters& p = CheckParametersOf(node->op());
        Type index_type = TypeOf(node->InputAt(0));
        Type length_type = TypeOf(node->InputAt(1));
        if (index_type.Is(Type::Integral32OrMinusZero())) {
          // Map -0 to 0, and the values in the [-2^31,-1] range to the
          // [2^31,2^32-1] range, which will be considered out-of-bounds
          // as well, because the {length_type} is limited to Unsigned31.
          VisitBinop(node, UseInfo::TruncatingWord32(),
                     MachineRepresentation::kWord32);
          if (lower() && lowering->poisoning_level_ ==
                             PoisoningMitigationLevel::kDontPoison) {
            if (index_type.IsNone() || length_type.IsNone() ||
                (index_type.Min() >= 0.0 &&
                 index_type.Max() < length_type.Min())) {
              // The bounds check is redundant if we already know that
              // the index is within the bounds of [0.0, length[.
              DeferReplacement(node, node->InputAt(0));
            }
          }
        } else {
          VisitBinop(
              node,
              UseInfo::CheckedSigned32AsWord32(kIdentifyZeros, p.feedback()),
              UseInfo::TruncatingWord32(), MachineRepresentation::kWord32);
        }
        return;
      }

其中这个VisitiBinop()这个函数不知道是干什么的。

但是这部分的逻辑已经很清楚了，它比较CheckBounds所检查的index Node的Range Type的最小值是不是大于0.0，然后检查最大值是不是小于length Node的Range Type的最小值，如果这两个部分都成立那么说明这次范围使用的index一定不会越界，那么这次的CheckBouds是冗余的直接将它删除。（在代码中是CheckBounds的第一个操作数也就是index Node直接替代CheckBounds）。

消除完之后SoN变成下面的样子：

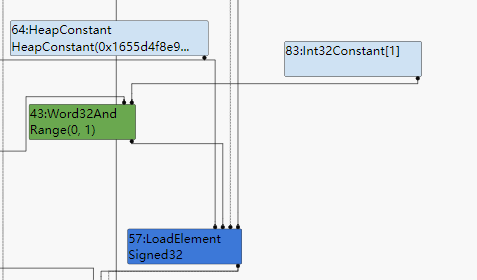
LoadElement已经直接使用Index作为操作数，看不到CheckBounds了。

Multiple Add Operation

之后再来了解一下turbofan中生成的各种加法Node，从这些Node的生成中也可以更加了解turbofan的推测优化以及，turbofan是如何对SoN中的Node进行化简。

SpeculativeSafeIntegerAdd

let opt_me = (x) => {
  return x + 1;
}

for (var i = 0; i < 0x10000; ++i)
  opt_me(i);
%DebugPrint(opt_me);
%SystemBreak();

在上面的例子中x + 1这个加法表达式会在bytecode graph builder阶段生成SpeculativeSafeIntegerAdd Node。

• 因为opt_me()在之前多次执行过程中向x传入的参数都是smi，导致加法的左操作数始终为smi类型。
• 加法的右操作数为1，所以右操作数也始终是smi类型。
• 而多次循环的计算结果也是smi。

上面的三个条件导致，在bytecode运行阶段由Ignition收集到的信息是这个加法所涉及的类型只有smi：

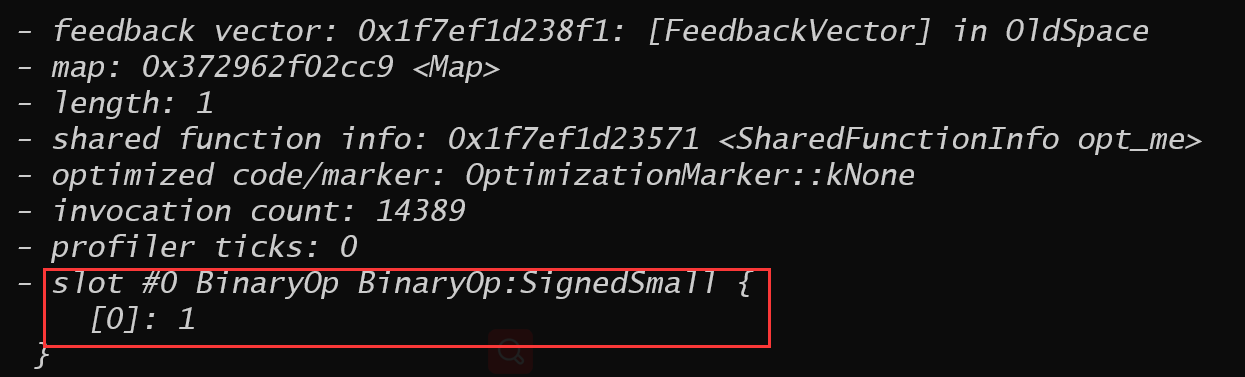
当这个函数进入turbofan优化时生成的是SpeculativeSafeIntegerAdd这个Node，之所以是Speculative的是因为这个Node的类型是由推测得到的。

下面是在Ignition中对AddSmi进行解释执行的handler：

// AddSmi <imm>
//
// Adds an immediate value <imm> to the value in the accumulator.
IGNITION_HANDLER(AddSmi, InterpreterBinaryOpAssembler) {
  BinaryOpSmiWithFeedback(&BinaryOpAssembler::Generate_AddWithFeedback);
}

从上面的handler的名字看出来AddSmi在执行的过程中也会收集feedback information。这也是为什么这样的优化被称为是推测优化，因为优化的整个过程是根据收集的feedback information做出假设进而然后针对假设的情况进行优化，一旦在执行的过程中传入不一样的操作数导致假设被推翻，将会触发deoptimization。

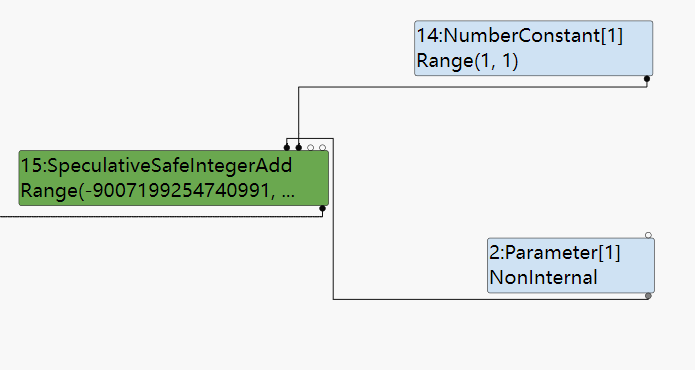
SpeculativeNumberAdd

SpeculativeNumberAdd这样的Node，可以在对下面程序的优化过程中出现。因为在opt_me()的加法表达式中右操作数的大小不在smi的范围内，导致生成的结点从上面的SpeculativeSafeIntegerAdd变成了SpeculativeNumberAdd（类型的变化是在一个lattice上前进）。

let opt_me = (x) => {
  return x + 1000000000000;
}
opt_me(42);
%OptimizeFunctionOnNextCall(opt_me);
opt_me(4242);

在Ingition中的feedback也看的很清楚：

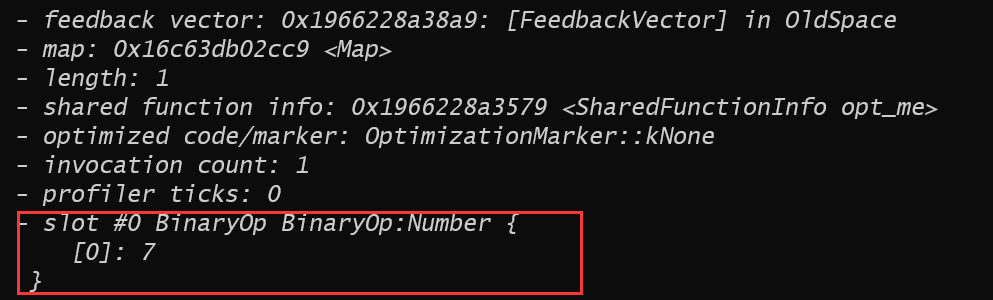
最终生成的turbofan也看的很清楚：

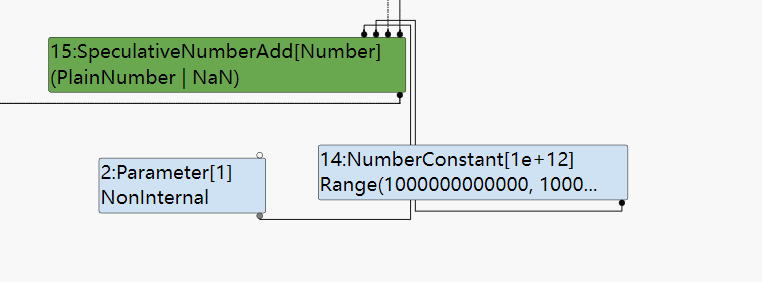
NumberAdd

let opt_me = (x) => {
  let y = x ? 10 : 20;
  return y + 100;
}

opt_me(true);
%DebugPrint(opt_me);
%OptimizeFunctionOnNextCall(opt_me);
opt_me(false);

上面这段代码中的opt_me()函数中的加法表达式在GraphBuild阶段按预期将会生成SpeculativeNumberAdd的Node来表示加法，但是当进入了typed lowering之后，turbofan会根据Node已经拥有的Type对一些Node进行化简。对于上面的例子来说：当turbofan意识到左操作数y的Type是Number类型且右操作数的类型是一个常数，这个时候可以很清楚的知道Node的类型一定是一个Number，而不需要进行任何推断，turbofan会将SpeculativeNumberAdd Node使用NumberAdd Node进行替换。

• typer阶段的SoN：

  

• typed lowering阶段的SoN：

  

Int32Add

let opt_me= (x) => {
  let y = x ? 10 : 20;
  return y + 100;
}
opt_me(true);
%OptimizeFunctionOnNextCall(opt_me);
opt_me(false);

和之前的例子一样opt_me()中的加法表达式在GraphBuild阶段应该生成SpeculativeSafeIntegerAdd Node，之后经历Typer、Typed Lowering（不知道为啥在Typed Lowering中没有把SpeculativeSafeIntegerAdd中的Speculative去掉？）、loop peeling……等等一系列的优化phase之后，会来到smplified lowering在这个phase中对已经经过优化的SoN中的结点再次进行Lowering。

在这个阶段中会进行TruncationPropagation（截断传播），对整个SoN进行数据流分析：为每个Node截断为合适的长度，并将截断信息进行传播。因为在上面的例子保证了SpeculativeSafeIntegerAdd 的操作数和结果都为smi，所以完全可以将这个结点截断到word32（32位），并用更简单的Node来替换这个高级的Node。所以在经历了smplified lowering之后SpeculativeSafeIntegerAdd 会变成 Int32Add。

simplified lowering之前：

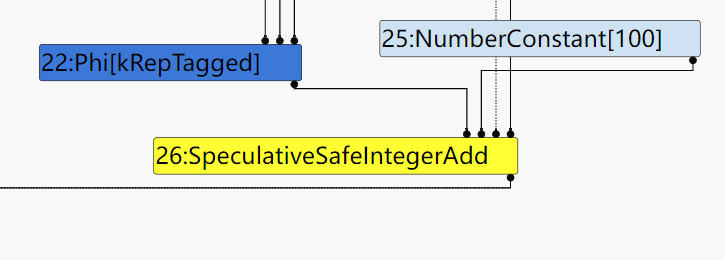
simplified lowering之后：

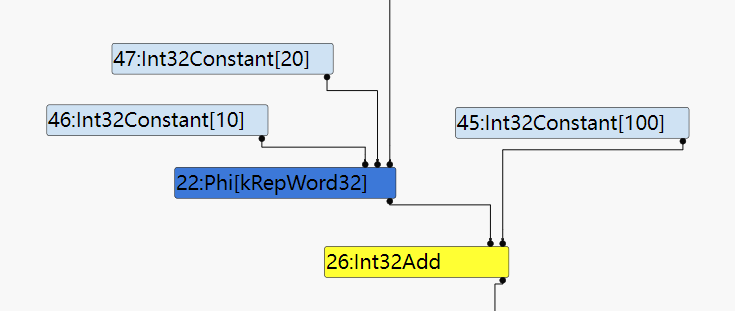
看到不但add的结点被替换掉了，而且Phi Node上也被传播上了截断信息。

JSAdd

let opt_me = (x) => {
  let y = x ? 
    ({valueOf() { return 10; }})
    :
    ({[Symbol.toPrimitive]() { return 20; }});
  return y + 1;
}

opt_me(true);
%OptimizeFunctionOnNextCall(opt_me);
opt_me(false);

在上面的例子中因为y是一个复杂的object所以turbofan生成一个JS层次的Node用来处理这种复杂的情况。

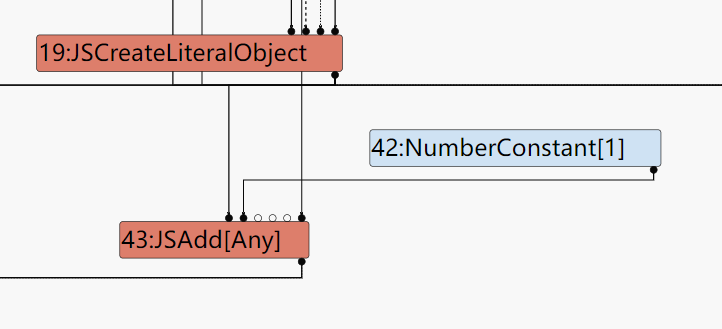
总结

到这里有关turbofan的介绍就告一段落。

这一部分是对turbofan的一些介绍，使用几个例子介绍了turbofan的优化过程。 首先对turbofan使用的IR SoN的特点以及生成SoN的意义做一下介绍。然后介绍Turbofan的Typer，介绍Turbofan是怎么样根据结点类型为每个Node打上Type。然后是Typed Lowering，观察turbofan怎么对拥有Type的Node进行化简。

之后是一些零散的知识，有关Range Type,以及CheckBounds。turbofan如何在Simpified Lowering阶段进行CheckBounds的消除。然后是对各种Add Node的介绍。