Fuzz with Grammar

Grammar Fuzzing Read Note

这一篇笔记是fuzzing book的syntactical fuzzing部分前三章的阅读笔记。

overview

之前了解过的基于变异的fuzzer，需要在fuzz之前提供测试用例，fuzzer对测试用例进行变异，将变异之后的测试用例输入到程序中。

但是一些程序中bug的触发依赖于输入中多种语法结构的组合，比如编译器，解释器。在对这些应用程序进行模糊测试时首先要保证语法的正确，否则程序在parsing阶段就会退出，无法触发到后面更多的程序逻辑。在使用基于变异的fuzz时，随机的变异是很难生成合法的语法结构，所以需要一种可以根据提供的语法规范生成输入的fuzzer——基于生成的fuzzer。

generation based on string operation

Grammar Fuzzer是在语法规则的指导下生成测试用例的，所以在构建一个Grammar Fuzzer的时候难免需要考虑两个问题：

• 使用什么样的形式R来表示语法规则。
• 在R这个表示形式之下，如何使用语法规则生成符合规则的输入。

在作者提供的第一种思路是使用map形式的巴克斯-诺尔范式（BNF）来表示语法规则。下面是使用BNF表示的算数表达式的语法规则：

EXPR_GRAMMAR: Grammar = {
    "<start>":
        ["<expr>"],

    "<expr>":
        ["<term> + <expr>", "<term> - <expr>", "<term>"],

    "<term>":
        ["<factor> * <term>", "<factor> / <term>", "<factor>"],

    "<factor>":
        ["+<factor>",
         "-<factor>",
         "(<expr>)",
         "<integer>.<integer>",
         "<integer>"],

    "<integer>":
        ["<digit><integer>", "<digit>"],

    "<digit>":
        ["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"]
}

整个语法规则被保存为一个map。每个产生式都是map中的一项，产生式的左部和产生式的右部都是字符串。非终结符用”<name>“的格式来表示。这样就解决掉”如何表示语法”这第一个问题了。之后需要考虑的问题就是：如何使用这样的语法规则来生成一系列的字符串，并作为程序的输入。

文章提出的第一种思路，直接使用字符串匹配和替换的方法，一个一个的将非终结符(symbol)替换为对应的扩展(expansion)，直到字符串中不存在非终结符。下面是具体的步骤：

• 所有的生成都是从开始符号开始，将开始符号保存在一个字符串S中。(”<start>“)
• 扫描S并用正则表达式”<[\^<>]>“匹配其中所有的非终结符,并将所有的非终结符保存在数组a中。
• 从a中随机选择一个非终结符n，并在语法规则的map中查找对应的产生式t。
• 从t的所有可选右部中随机选取一个s（也是一个字符串毫无疑问），并用s替换n在S中所占据的位置。这样n就被展开了一次。
• 回到2继续，直到S中找不到非终结符，或者满足了某些限制条件，停止。

使用上面的方法就可以从<start>开始生成一条符合语法规则的输入。下面是对应的python代码：

def simple_grammar_fuzzer(grammar: Grammar, 
                          start_symbol: str = START_SYMBOL,
                          max_nonterminals: int = 10,
                          max_expansion_trials: int = 100,
                          log: bool = False) -> str:
    """Produce a string from `grammar`.
       `start_symbol`: use a start symbol other than `<start>` (default).
       `max_nonterminals`: the maximum number of nonterminals 
         still left for expansion
       `max_expansion_trials`: maximum # of attempts to produce a string
       `log`: print expansion progress if True"""

    term = start_symbol
    expansion_trials = 0

    while len(nonterminals(term)) > 0:
        symbol_to_expand = random.choice(nonterminals(term))
        expansions = grammar[symbol_to_expand]
        expansion = random.choice(expansions)
        # In later chapters, we allow expansions to be tuples,
        # with the expansion being the first element
        if isinstance(expansion, tuple):
            expansion = expansion[0]

        new_term = term.replace(symbol_to_expand, expansion, 1)

        if len(nonterminals(new_term)) < max_nonterminals:
            term = new_term
            if log:
                print("%-40s" % (symbol_to_expand + " -> " + expansion), term)
            expansion_trials = 0
        else:
            expansion_trials += 1
            if expansion_trials >= max_expansion_trials:
                raise ExpansionError("Cannot expand " + repr(term))

    return term

为了防止在处理某些递归语法的过程中陷入终结符数量无法减少的情况，上面的算法还限制了扩展的总数。这个函数所产生的符合语法规则的字符串还可以被进一步送入到基于变异的fuzzer中进行少量的变异，希望在经过变异之后的测试用例可以触发某些边界情况。

generation based on tree operation

对于基于字符串操作的fuzzer，文章提出了两个问题：

• 工作效率低：在fuzzer工作过程中伴随着大量的字符串匹配和字符串替换的操作，这样的操作一开始效率就不高，伴随着整个字符串S的不断扩展和变长将会变得越来越低效。
• 难以控制：很难在字符串这样的扩展载体上附加一些控制信息，和回溯整个扩展的过程。

为了追求更高的效率和更复杂的功能，文章提出用语法树来表示语法结构。使用树一方面可以提高扩展的效率，另一方面可以让我们对扩展的过程有更好的控制。

the structure of tree

接下来的问题就是如何在fuzzer中表示语法树。语法中的每一个符号不管是终结符还是非终结符都将被表示为树中的一个node。

因为文章中使用是python来实现fuzzer，所以将node被表示为下面这样的元组：

(SYMBOL_NAME, CHILDREN)

其中SYMBOL_NAME是一个字符串，代表了符号的名字：”<start>”, +，而CHILDREN是一个python list，代表了这个node的所有子节点（node的子节点代表了node被拓展之后的表示）。

CHILDREN除了保存子节点之外还可以有两种特殊的取值：

• 当CHILDREN为[]，这个node是一个终结符。
• 当CHILDREN为None，这个node是一个非终结符但是还未拓展。（可以被拓展，叶子节点）

所以下面这段代码所生成的语法树：

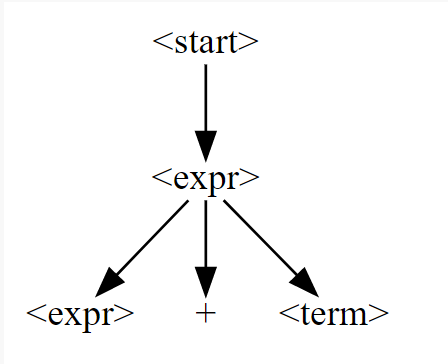
derivation_tree: DerivationTree = ("<start>",
                   [("<expr>",
                     [("<expr>", None),
                      (" + ", []),
                         ("<term>", None)]
                     )])

打印出来之后是这个样子：

how to expand the tree

在解决完如何表示语法规则这个问题之后，就需要解决如何使用语法树这个结构来拓展语法规则的问题。

语法树从一个开始符号开始拓展，这个开始符号默认为”<start>“。

• [1] 首先遍历整个语法树，寻找树中还未拓展的非终结符节点n，也就是CHILDREN为None的节点。遍历的过程是下面这样的：
  • 对于遍历到的每个节点n’，先判断这个节点的CHILDREN是否为None，如果是，那么这个这个节点就可以当作n，跳转到[2]对n进行扩展，如果不是继续下面的逻辑。
  • 对n’的每个孩子c调用any_possible_expansions()这个函数，判断以c为根节点的这棵子树中是否还有可以被扩展的非终结符节点。并将所有返回值为true的c保存在一个list l中。
  • 从l中随机选择一个孩子c’,然后以c’作为n’继续这个过程，直到找到一个CHILDREN为None的节点n’。(在这一步如果n’是终结符或者，或者n’的所有子树都无法再被扩展（一般不会有这种情况因为外层还会有检查），那么l为空，会直接跳转到[4]返回原本的语法树，代表这棵树没有办法再被扩展)。

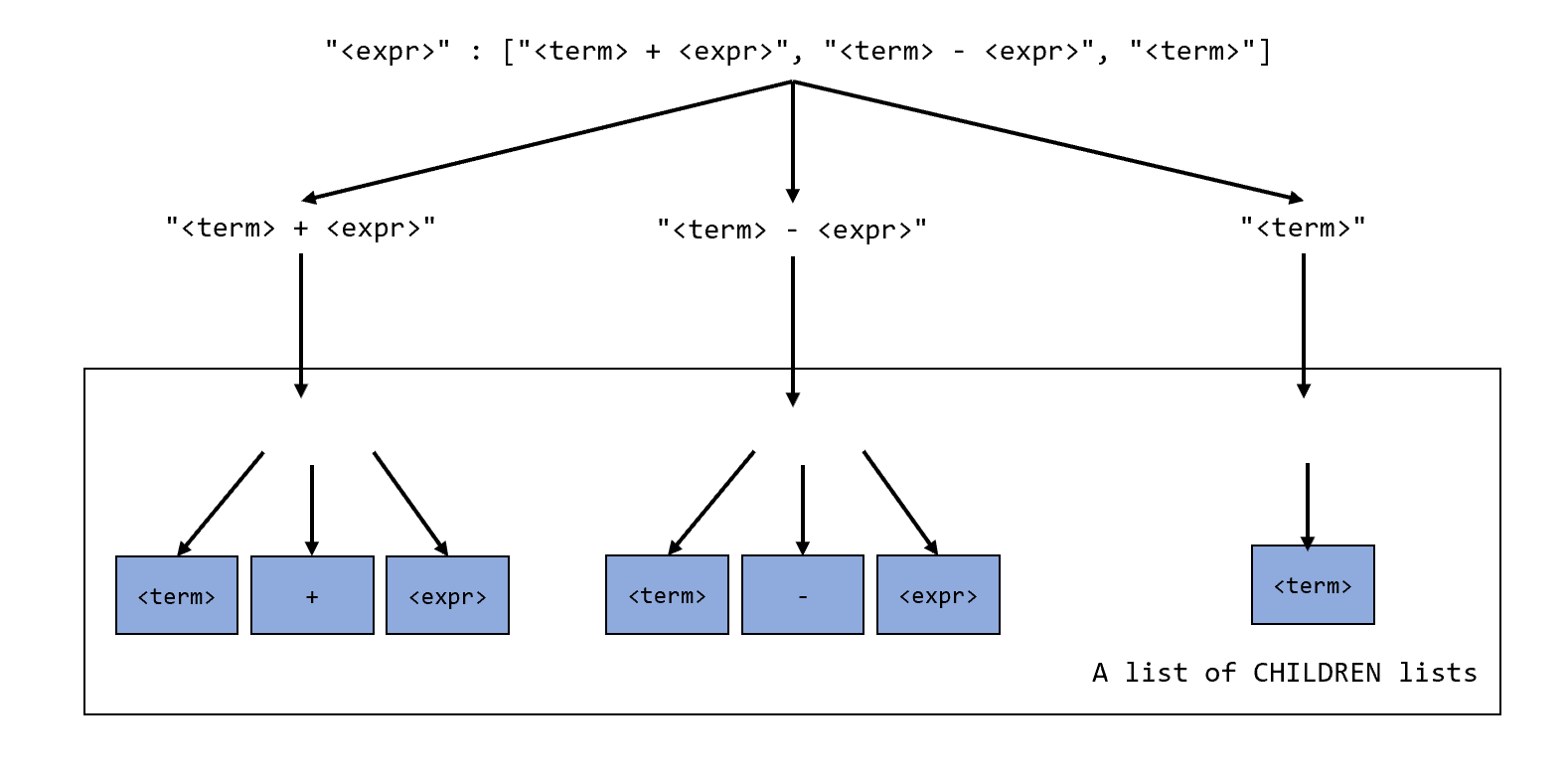
• [2] 取出n的symbol到grammar中去找到它对应的产生式。将产生式中所有的可选扩展转换为树的形式。下面是将”<expr>“对应产生式转换为树形式的结果：

  

​ 最终转换的结果是一个list其中保存了，所有备选的CHILDREN list。

• [3] 从这些所有的children中随机选择一个children并赋值给n的CHILDREN字段，这样n就被扩展完成了。
• [4] 返回这棵被扩展之后的语法树。

下面是用python所实现的整个扩展算法：

def expand_tree_once(self, tree: DerivationTree) -> DerivationTree:
        """Choose an unexpanded symbol in tree; expand it.
           Can be overloaded in subclasses."""
        (symbol, children) = tree
        if children is None:
            # Expand this node
            return self.expand_node(tree)

        # Find all children with possible expansions
        expandable_children = [
            c for c in children if self.any_possible_expansions(c)]

        # `index_map` translates an index in `expandable_children`
        # back into the original index in `children`
        index_map = [i for (i, c) in enumerate(children)
                     if c in expandable_children]

        # Select a random child
        child_to_be_expanded = \
            self.choose_tree_expansion(tree, expandable_children)

        # Expand in place
        children[index_map[child_to_be_expanded]] = \
            self.expand_tree_once(expandable_children[child_to_be_expanded])

        return tree

到现在为止已经可以使用树作为表示形式来扩展语法，但是没有解决的问题是如何控制扩展的过程，避免出现扩展无法停止（也就是无限递归）的情况。

closing the expansion

为了解决上面的问题，我们需要的是一种可以让拓展停止下来的方法。

文章认为每次扩展语法树都会为语法树之后的扩展带来代价（cost）。举例来说，假如在扩展的过程中，我们需要对<expr>这个非终结符进行扩展：

"<expr>" : ["<term> + <expr>", "<term> - <expr>", "<term>"],

而在这一次对<expr>的扩展中选择”<term> + <expr>“作为孩子。那么这一次扩展所带来的cost = 将这个扩展之后的结果”<term> + <expr>“再完全扩展（扩展到不存在非终结符）所需要的扩展次数 + 1（这一次扩展）。cost衡量了在一次扩展的过程之后为语法树所引入的复杂度。这意味如果想要扩展次数尽可能的少，或者想要扩展尽可能早的结束在每次扩展时我们需要选择cost最小的children。

文章提供的思路是：在一开始先让语法树正常的进行扩展（也就是不对扩展进行控制），等到语法树中非终结符的数量达到一个阈值（表明语法树已经足够复杂），之后的每次扩展都选择cost最小的children进行展开，这样就保证了expansion可以正常结束。

为了实现上面的逻辑，需要引入两个cost：

• symbol cost：将一个非终结symbol完全扩展为终结符所需要的最小扩展次数。
• expansion cost：将一个expansion完全扩展为终结符需要的扩展次数（就是上面所描述的cost）。数值等于expansion中所有非终结符symbol cost的总和 + 1。特殊情况是如果expansion中没有非终结符，expansion cost 等于1，因为只需要扩展他自己这一次就会结束。

下面是计算这两个cost的算法实现:

    def symbol_cost(self, symbol: str, seen: Set[str] = set()) \
            -> Union[int, float]:
        expansions = self.grammar[symbol]
        return min(self.expansion_cost(e, seen | {symbol}) for e in expansions)

    def expansion_cost(self, expansion: Expansion,
                       seen: Set[str] = set()) -> Union[int, float]:
        symbols = nonterminals(expansion)
        if len(symbols) == 0:
            return 1  # no symbol

        if any(s in seen for s in symbols): #recursive
            return float('inf')

        # the value of a expansion is the sum of all expandable variables
        # inside + 1
        return sum(self.symbol_cost(s, seen) for s in symbols) + 1

在代码中可以看到，在计算expansion cost的过程中如果遇到了递归的情况，cost会直接被设置为infinite，这样有递归情况发生的扩展规则就会被舍弃（除非一个symbol的所有expansion都存在递归XD）。

在之前所实现的fuzzer中，在扩展非终结符时会从所有可选的children中随机选择一个children作为扩展。但是现在我们有了cost，就可以根据cost选择合适的children。文章中提高的拓展思路是这样的：

• 在进行拓展时有两个限制变量：min_nonterminals，max_nonterminals。
• 首先，在每次扩展时选择expansion cost最大的children，直到整个语法树中的非终结符数量到达min_nonterminals。
• 然后，在每次扩展时使用随机的策略选择children，直到整个语法树中的非终结符数量到达max_noterminals。
• 最后，在每次扩展时选择expansion cost最小的children，直到整个语法树中的非终结符数量为0，扩展结束。

使用这样的扩展策略，保证在最后的阶段扩展是可以停止的，避免了随机扩展可能出现的无限递归的情况。下面是按照expansion来选择children的python实现：

def expand_node_by_cost(self, node: DerivationTree, 
                            choose: Callable = min) -> DerivationTree:
        (symbol, children) = node
        assert children is None

        # Fetch the possible expansions from grammar...
        expansions = self.grammar[symbol]

        children_alternatives_with_cost = [(self.expansion_to_children(expansion),
                                            self.expansion_cost(expansion, {symbol}),
                                            expansion)
                                           for expansion in expansions]

        costs = [cost for (child, cost, expansion)
                 in children_alternatives_with_cost]
        chosen_cost = choose(costs)
        children_with_chosen_cost = [child for (child, child_cost, _) 
                                     in children_alternatives_with_cost
                                     if child_cost == chosen_cost]
        expansion_with_chosen_cost = [expansion for (_, child_cost, expansion)
                                      in children_alternatives_with_cost
                                      if child_cost == chosen_cost]
		# random choose a children with same cost
        index = self.choose_node_expansion(node, children_with_chosen_cost)

        chosen_children = children_with_chosen_cost[index]
        chosen_expansion = expansion_with_chosen_cost[index]
        chosen_children = self.process_chosen_children(
            chosen_children, chosen_expansion)

        # Return with a new list

fuzzing with grammar coverage

上面的部分讨论了两种使用语法生成测试用例的fuzzer的构建方法。为了使fuzzer的功能更加强大，在这一部分要讨论的内容是：如何使fuzzer生成的测试用例可以更快，更全面的覆盖到全部的语法规则，提高语法的多样性并且不遗漏个别元素。

首先这部分内容中所提到的语法规则覆盖率中的语法规则指的不是产生式，而是产生式中所有可选的语法规则。比如下面这个产生式可以被分解为三条语法规则：

"<expr>" : ["<term> + <expr>", "<term> - <expr>", "<term>"]

	<expr> -> <term> + <expr>
	<expr> -> <term> - <expr>
	<expr> -> <term>

closing the expansion这一章所实现的fuzzer在扩展非终结符时，根据所有可选children的expasnsion cost决定哪个是[1]合适的children，如果有多个children的expansion cost一样且都符合要求，那么将从这些都符合要求的children组成的list中随机选择[2]一个children作为最终的扩展。而在这一部分将对标号为[2]的随机的选择进行改进：不是随机选择，而是从符合要求的children list中选择一个能提高语法覆盖率的children作为最终的扩展。

对于如何从符合要求的children list中选择一个能够提高语法覆盖率的children，文章给出了两种方法。

look expansion only

这个方法一共分为下面几步：

• 首先调用uncovered_children()从children list中筛选出所有还未被覆盖的children。
• 如果所有的children都被覆盖掉那么，回到最初的随机选择方法。
• 否则，从所有未被覆盖的children中随机选择一个children作为最终的扩展，并将这个children对应的语法规则加入到已覆盖的语法规则中。

第一种方法比较直接，它的核心思想是：在从children list选择children时，观察的指标就是这个children对应的语法规则是否被覆盖过。fuzzer更倾向于，在扩展中使用没有被覆盖过的语法规则，而如果所有可选的语法规则都已经被覆盖，那么只能随机的选择一条语法规则进行扩展。

举个例子，假如正在被扩展的是<expr>这个非终结符：

"<expr>" : ["<term> + <expr>", "<term> - <expr>", "<term>"]

[1] <expr> -> <term> + <expr>
[2] <expr> -> <term> - <expr>
[3] <expr> -> <term>

<expr>总共有上面三个可选的children，假设其中[1]和[2]是符合expansion cost的需求的，再假设只有[1]是未被覆盖过的规则。最终选择的children就只能是<term> + <expr>。

相比较于在扩展时随机选择children，使用这种方法选择children已经可以在一定程度上提高所产生测试用例的语法覆盖率。下面是这个方法的python实现：

    def choose_node_expansion(self,
                              node: DerivationTree,
                              children_alternatives: List[List[DerivationTree]]) -> int:
        """Return index of expansion in `children_alternatives` to be selected.
           Picks uncovered expansions, if any."""

        # Prefer uncovered expansions
        (symbol, children) = node
        uncovered_children = [c for (i, c) in enumerate(children_alternatives)
                              if expansion_key(symbol, c)
                              not in self.covered_expansions]
        index_map = [i for (i, c) in enumerate(children_alternatives)
                     if c in uncovered_children]

        if len(uncovered_children) == 0:
            # All expansions covered - use superclass method
            return self.choose_covered_node_expansion(node, children_alternatives)

        # Select from uncovered nodes
        index = self.choose_uncovered_node_expansion(node, uncovered_children)

        return index_map[index]

但是这种方法也有一个问题：对于children的观察和判断不够深入。举一个例子来说：

"<letter>" : ["<plus>'", "<percent>", "<other>"]

[1] <letter> -> <plus>
[2] <letter> -> <percent>
[3] <letter> -> <other>

假设<letter>的三个children都是符合条件的children且这三个children的规则都已经被覆盖过，那么按照第一种方法，将会对这三个children平等对待，从这三个children中随机选择一个children扩展，但实际上这三个children可能不是平等的。 这种方法只考虑到这一次扩展对语法覆盖率带来的改变，而没有考虑到后续扩展对语法覆盖率的影响。可能出现的一种情况是，如果继续扩展<percent>，在扩展<percent>的过程中可能会遇到未被覆盖的语法规则，而另外两个无论如何扩展后续的语法规则都是已经被覆盖过的。这就意味着，如果选择<percent>可能会带来更大的语法覆盖率。

之所以出现这样的问题是因为第一种方法是短视的，它只观察这一次扩展的所使用的语法规则是否被覆盖过，而不继续向下观察。而第二种方法就是为了解决这个问题。

deep foresight

为了解决上面提出的问题，我们必须观察的足够深入才行。

在为一个非终结符T的扩展选择children时，对于一个children C，不能只观察T->C是否被覆盖过，还要观察将C展开过程中所使用的未被覆盖的语法规则（n），如果n不为空就意味着选择这个C可能会带来更大的语法覆盖率。

计算的公式是：n = 展开C途中使用的语法规则（p） - 已经被覆盖过的语法规则(q)

• 为了实现这个目的，在每次扩展时，需要计算每个备选children扩展途中所可能使用的语法规则(p)，可以使用下面的函数进行计算：

  def max_expansion_coverage(self, symbol: str, 
                              max_depth: Union[int, float]) -> Set[str]:
      if max_depth <= 0:
          return set()
    
      self._symbols_seen.add(symbol)
    
      expansions = set()
      for expansion in self.grammar[symbol]:
          expansions.add(expansion_key(symbol, expansion))
          for nonterminal in nonterminals(expansion):
              if nonterminal not in self._symbols_seen:
                  expansions |= self._max_expansion_coverage(
                      nonterminal, max_depth - 1)
    
      return expansions
  

​ max_expansion_coverage()函数接受一个非终结符，返回在扩展这个非终结符到深度depth过程中使用语法规则。要计算扩展一个children使用的语法规则只需要对children中所有的非终结符调用这个函数，再将结果全部并起来就可以了。

• 而q在每次扩展的时候就已经统计好了，所以此时p - q得到的就是n。

      def new_child_coverage(self,
                             symbol: str,
                             children: List[DerivationTree],
                             max_depth: Union[int, float] = float('inf')) -> Set[str]:
          """Return new coverage that would be obtained 
             by expanding (`symbol`, `children`)"""
    
          new_cov = self._new_child_coverage(children, max_depth)
          new_cov.add(expansion_key(symbol, children))
          new_cov -= self.expansion_coverage()   # -= is set subtraction
          return new_cov
    
      def _new_child_coverage(self, children: List[DerivationTree],
                              max_depth: Union[int, float]) -> Set[str]:
          new_cov: Set[str] = set()
          for (c_symbol, _) in children:
              if c_symbol in self.grammar:
                  new_cov |= self.max_expansion_coverage(c_symbol, max_depth)
    
          return new_cov
  

在可以计算n的基础上，我们可以得到一个深度优先的children选择算法，在选择children时：

• 对每个children从depth = 0开始计算n。
• 递增depth，直到depth = d，有children的n不为空。
• 将这个depth = d下所有children的n保存在一个列表l中。l代表了每个children在扩展到d这个深度时，使用的未被覆盖的语法规则。
• 选择n的size最大的children作为最终扩展的children，可以为测试用例带来最大的语法覆盖率。

第二种方法在扩展时，不仅更倾向于选择能立即增加语法覆盖率的children，而且倾向于选择可能能增加语法覆盖率的children。

coverage with context

到现在为止，我们已经拥有了可以在生成测试用例的过程中不断提高语法覆盖率的fuzzer。但是在计算语法覆盖率时，我们只考虑了单条的语法规则A->B是否被使用，而没有考虑到一条语法规则可以在不同的上下文中使用，同一条语法规则在不同的上下文中使用也应该算作不同的语法规则。

还是举例子来说明：

'<factor>' : ['+<factor>', '-<factor>', '(<expr>)', '<integer>.<integer>', '<integer>']

在上面的语法规则中，有多处位置使用了<integer>这个非终结符，如果使用我们上面设计的fuzzer生成测试用例，fuzzer可以保证在生成测试用例的过程中覆盖到由<integer>派生出的所有语法规则，但是这些被覆盖的语法规则将分布在<integer>出现的每一个地方。之前所设计的fuzzer不能保证在<integer>出现的每个地方都覆盖所有派生的语法规则，它是上下文不敏感的。

为了使fuzzer可以使用上下文敏感的语法覆盖率引导，我们需要将在不同位置出现的相同符号区分开，就像静态分析的中的上下文敏感指针分析一样我们要为出现的每个非终结符添加上下文信息，来区别这些非终结符。

具体的做法就是改变非终极符的名字，对于上面的语法来说在添加上下文信息之后得到的是下面的语法规则：

'<factor>': ['+<factor>','-<factor>','(<expr>)','<integer-1>.<integer-2>','<integer>'],
'<integer>': ['<digit><integer>', '<digit>'],
'<digit>': ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'],
'<integer-1>': ['<digit-1><integer-1>', '<digit-2>'],
'<digit-1>': ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'],
'<digit-2>': ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'],
'<integer-2>': ['<digit-3><integer-2>', '<digit-4>'],
'<digit-3>': ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'],
'<digit-4>': ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9']

我们需要了解添加上下文的逻辑并将这个逻辑自动化：

• <integer>被添加了后缀变成<integer-X>，后缀代表他的上下文信息，也将它和其它<integer>区分开。

• <integer-X>将被复制一份和<integer>相同的语法规则，在上面的例子将复制一份下面的语法规则：

  '<integer-1>': ['<digit><integer>', '<digit>']
  

• 之后我们将递归为这些所有复制的语法规则添加上下文信息。在这个过程中对于已经复制过一次的非终极符不再重新复制，比如<integer>这个非终结符已经被复制为<integer-1>那么在处理<integer-1>复制得到的语法规则时，<integer>这个非终结符不会再次被复制为<integer-1-1>，这样做的原因是为了避免出现无限递归。（<integer-1-1>里还会有<integer-1-1-1>以此类推就不会停止下去了，这样做的当然会损失一部分上文信息）

下面是这个上文信息添加算法的python实现：

def _duplicate_context(grammar: Grammar,
                       orig_grammar: Grammar,
                       symbol: str,
                       expansion: Optional[Expansion],
                       depth: Union[float, int],
                       seen: Dict[str, str]) -> None:
    """Helper function for `duplicate_context()`"""

    for i in range(len(grammar[symbol])):
        if expansion is None or grammar[symbol][i] == expansion:
            new_expansion = ""
            for (s, c) in expansion_to_children(grammar[symbol][i]):
                if s in seen:                 # Duplicated already
                    new_expansion += seen[s]
                elif c == [] or depth == 0:   # Terminal symbol or end of recursion
                    new_expansion += s
                else:                         # Nonterminal symbol - duplicate
                    # Add new symbol with copy of rule
                    new_s = new_symbol(grammar, s)
                    grammar[new_s] = copy.deepcopy(orig_grammar[s])

                    # Duplicate its expansions recursively
                    # {**seen, **{s: new_s}} is seen + {s: new_s}
                    _duplicate_context(grammar, orig_grammar, new_s, expansion=None,
                                       depth=depth - 1, seen={**seen, **{s: new_s}})
                    new_expansion += new_s

            grammar[symbol][i] = new_expansion

• grammar：全部语法规则（在添加上下文是这个语法规则将被修改）。
• orig_grammar：原本的语法规则，和上面的语法规则值是一样的但是不会被修改，只是在复制的时候用来获取原本的语法。
• symbol：symbol的孩子将被添加上下文信息。
• expansion：symbol具体哪一个孩子被添加语法信息。
• depth：递归添加上下文信息的深度。
• seen：已经添加了上下文信息的非终结符（避免无限递归）。

对语法规则中的所有非终结符调用上面的函数并传入expansion为空就可以为所有语法规则添加上下文信息。这样再使用之前的fuzzer处理之后的语法上生成测试用例，就可以使用上下文敏感的语法覆盖率进行引导。